函数式思维 - Part 2

Part 2：组合跨世界方法

我们经常会遇到跨世界的方法：

• 用id去数据库查数据，有可能查不出来：String -> Option<User>
• 把String转为Integer，有可能出错：String -> Try<Integer>
• 爬虫根据url异步的拉取网页：String -> Async<Page>

这种跨世界的方法很好识别，他们的类型都是：a -> E<b>;

在N世界里的方法我们可以组合起来：a -> b和b -> c组合就是a -> c；但是跨世界的方法我们却没法组合：

举个例子，我有个String，要转成Int，再拿Int去数据库查User：String -> Option<Int>和Int -> Option<User>是没法组合的。

在有null的语言里你可以写String -> Int和Int -> User，虽然它俩可以组合，但是里面有非null判断，说不定还要抛异常（异常可以理解成特殊的返回值），其实是隐藏了多个返回值，这种代码是很难抽象和维护的。

bind

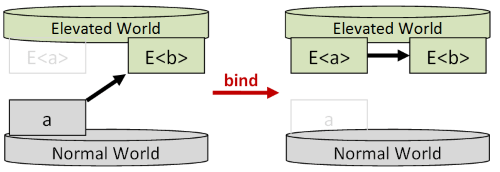
• 常见方法名：bind, flatMap, andThen, collect, SelectMany, >>=, =<<
• 作用：把跨世界函数变成E时间函数，可以借此组合跨世界（monadic）的函数
• Signature：(a->E<b>) -> E<a> -> E<b>
• Signature变种：E<a> -> (a->E<b>) -> E<b>

虽然跨世界的函数本身不能组合，但是如果我们把他们都bind到E世界，就能在E世界组合了：

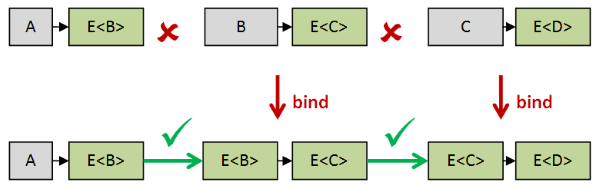
bind另一种理解方式是一个两参函数，把a->E<b>应用到把E<a>拆开的a上，得到E<b>:

// ('a -> 'b option) -> 'a option -> 'b option
module Option =
    let bind f xOpt =
        match xOpt with
        | Some x -> f x
        | _ -> None

// ('a -> 'b list) -> 'a list -> 'b list
module List =
    let bindList (f: 'a->'b list) (xList: 'a list)  =
        [ for x in xList do
          for y in f x do
              yield y ]

就拿上面那个的String要转成Int，再拿Int去查数据库举个例子：

// string -> int option
let parseInt str =
  match str with
  | "-1" -> Some -1
  | "0" -> Some 0
  | "1" -> Some 1
  | _ -> None

// User类型，这里简化一下，只有id
let User = User of int

// int -> User option
let toUser id =
    if id >= 0 then     // 不允许负数
        Some (User id)  // 假装查数据库
    else
        None

有了bind我们就能直接生成一个接收string并返回User option的函数：

// string -> User option
let getUser str =
    parseInt str
    |> Option.bind toUser

注意getUser本身又是一个跨世界函数，还可以继续bind。

和map/apply一样，我们有个bind的中缀版>>=：

let getUser_2 str =
    str |> parseInt >>= toUser

bind有时被称作FP界的分号，因为bind连起来的话有点像你写Java的时候写的分号：

expression1 >>=
expression2 >>=
expression3 >>=
expression4

statement1;
statement2;
statement3;
statement4;

这种连写很常见，所以很多FP语言都做了语法糖来简化它：

// Scala
for {
    x <- initialExpression
    y <- expressionUsingX(x)
    z <- expressionUsingY(y)
} yield {
    x+y+z
}

-- Haskell
do
    x <- initialExpression
    y <- expressionUsingX x
    z <- expressionUsingY y
    return x+y+z

Bind vs. Apply vs. Map

bind/return组合要比apply/return组合要“更强”，因为有了bind/return就能定义出map和apply，反之则不行。

如图是map用bind的实现，map f xs = xs >>= return . f：

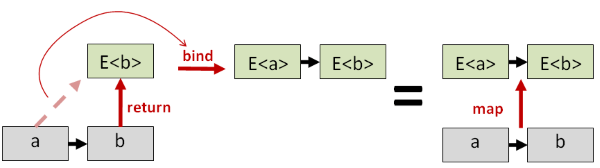
举个Option的例子：

// Option的map用bind的实现
let map f =
    Option.bind (f >> Some)

// Option的apply用bind的实现1
let apply fOpt xOpt =
    fOpt |> Option.bind (fun f ->
        let map = Option.bind (f >> Some)
        map xOpt)

// Option的apply用bind的实现2，和上面的等价
let apply fOpt xOpt =
    fOpt >>= (fun f ->
        xOpt >>= (f >> Some))

apply的实现简单说下：

• apply的类型：E<a->b> -> E<a> -> E<b>，第一个参数是fOpt，第二个参数是xOpt
• bind的类型：(f -> E<b>) -> E<f> -> E<b>，其中f是a -> b，于是就有(a->b->E<b>) -> E<a->b> -> E<b>
• 第一个参数(a->b) -> E<b>参数就是f，返回值是E<b>，可以用map搞出来：a->b -> E<a> -> E<b>是map，直接map f xOpt就行了，map又可以用bind实现，就是xOpt >>= (f >> Some)

上面的实现2用语法糖写就很通俗易懂了，下面是Haskell的实现：

apply fOpt xOpt = do
   f <- fOpt
   x <- xOpt
   return (f x)

很好理解，把E<a->b>里的a->b“拿出来”，再把E<a>里的a“拿出来”，然后把a应用到a->b上得到b，最后“塞到”E里得到E<b>。

和map、apply一样，bind/return也要遵循一些规则，这些规则叫做Monad Laws；有apply/return方法并满足这些规则的叫做Monad。

如下是其中的3个规则：

• bind return 和 id 应该是一样的：
  
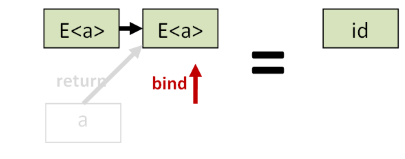
• apply (bind f) (return a) 和 apply f a 应该是一样的，bind和return不应该改变数据本身：
  
  
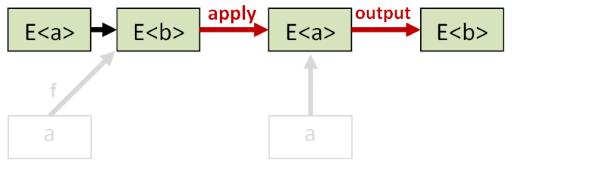
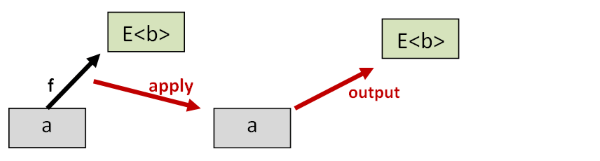
• (a >>= f) >>= g 和 a >>= (fun x -> f x >>= g) 应该是一样的，这个说的就是bind满足结合律（和普通方法一样 g(f(a))和(g . f) a应该是一样的）

Summary

这章讲了如何用bind组合跨世界的方法，下章说说什么时候用apply，什么时候用bind。

注意类型本身不是Monad – 不能说List/Optional是Monad，而是实现了bind和return并且满足Monad Law的才叫Monad。

留一个有趣的问题：JavaScript的Promise是不是Monad？Promise提供了then和resolve方法，分别对应bind和return，你可以自己证明试试。