函数式思维 - Part 1

前言

软件开发很大程度上是在做抽象，把摸不着的东西抽象成实在的东西，把复杂的东西抽象成简单的东西，比如程序语言本身就是最原始的抽象，谁也不想用汇编来写业务代码，不同语言选择了不同的抽象方式：

• 有的语言选择了以类为主的抽象，叫做OOP，它们依赖维护和改变类的状态来代表程序；
• 有的语言选择了以函数为主的抽象，叫做FP，它们依赖函数输入输出来代表程序；

当你用OOP语言的时候，你当然可以选择不用语言提供的抽象能力，比如一个多的类我都不定义，所有程序都在main方法里堆着，当然这样程序基本上就没法维护了。所以你需要借助OOP的能力来：

• 操作基本类型；
• 组合基本类型成复杂的类，再由复杂的类组合成更复杂的类，并在其上定义方法去操作他们；

因为大多数OOP语言里的第一公民都是类，所以你需要抽象的是怎么操作、组合类。

同理在第一公民是函数的FP语言里，你需要抽象的是怎么操作、组合函数。

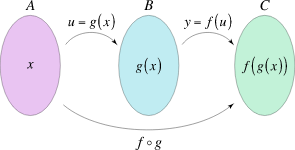
最简单的函数组合例子：

虽然你可以定义无数个各不相同的函数，但是他们还是有一些共性我们能抽象出来，来更好的操作、组合它们，可以说他们是FP界的设计模式。但是这些抽象比OOP里的设计模式要更加抽象，实现更单一，也不和特定语言绑定，基本上OOP里的设计模式到了FP就都是函数了。这也就是为什么很多OOP语言里都借鉴实现了FP里的概念，反之则很少。

---

TLDR：

这篇文章主要讲解函数式里的常见概念，虽然这些概念和特点语言没有关系（更多的是和Category Theory有关），但是很多语言都借鉴并实现了这些概念（比如Haskell、Scala），希望最后能帮助你Thinking in Functional，比如：

一些“类”：

• Functor
• Applicative
• Monad
• Traversable

一些方法：

• map
• return
• apply
• liftN
• zip
• bind
• traverse / mapM
• sequence

Backgroud

我们假设程序能运行在两个世界中，normal（后面简称N）和elevated（后面简称E）：

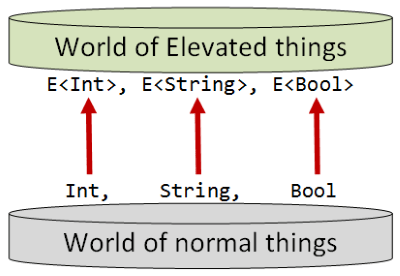
如上图，在N世界中我们有一些值，其类型是Int，那么在E世界中同样有对应的一些值E<Int>；

同样的逻辑也可以应用在函数（function）上：

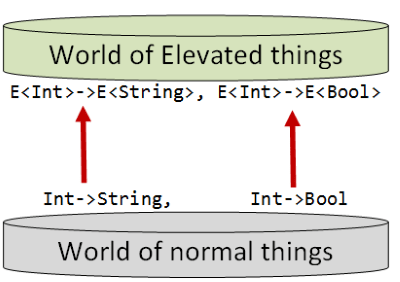
如图，如果我们在N世界中有个接受Int输出String的函数，那么在E世界中同样对应也有接受E<Int>并输出E<String>的函数。

Elevated世界

E世界包含了很多东西，比如数据结构（Option<T>，List<T>），比如异步（Async<T>）等等；虽然他们都不相同，但是他们都在elevated世界，如果我们对付elevated世界有相同的方法，那他们也有共性。

Part 1： Lifting to the elevated world

lifting：把N世界的移到E世界中：

• lift types：每个N世界的类型在E世界中都有一个对应的类型；
• lift values：每个N世界的值在E世界中都有一个对应的值；
• lift functions：每个N世界的函数在E世界中都有一个对应的函数；

虽然每个E世界都不一样，不可能有一个统一的lift实现，但是这个lift行为本身我们可以起一个统一的名字：比如map、return。

map

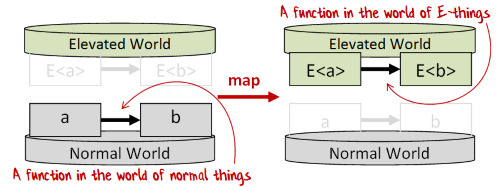
• 常见方法名：map, fmap, lift, select, <$>, !
• 作用：lift一个方法到E世界;
• Signature：(a->b) -> E<a> -> E<b>
• Signature变种：E<a> -> (a->b) -> E<b>，可以理解成一个两参函数，把a->b应用到E<a>上得到E<b>）
  

在大多数支持currying的语言里，这两个Signature是一样的

下面左边是F#（F#是ML的一个方言)实现Option/List的例子；右边是Java库里的实现：

// ('a -> 'b) -> 'a option -> 'b option
let mapOption f opt =
    match opt with
    | None ->
        None
    | Some x ->
        Some (f x)

// ('a -> 'b) -> 'a list -> 'b list
let rec mapList f list =
    match list with
    | [] ->
        []
    | head::tail ->
        // new head + new tail
        (f head) :: (mapList f tail)

// Optional.java
public <U> Optional<U>
map(Function<? super T, ? extends U> mapper) {
    //...
}

// Stream.java
<R> Stream<R>
map(Function<? super T, ? extends R> mapper);

可以看到虽然Java是OOP的，F#是FP的，但是他们的Signature却是一样的，比如第一个，Java也是(T->U) -> Optional<T> -> Optional<U>：一个参数是一个T->U函数；另一个参数是this，也就是调用map的实例，其类型是Optinoal<T>；返回类型是Optional<U>；

OOP里所有的方法（非static）如果换个角度看的话，都自带一个this参数；

有了map我们就可以把N世界的方法lift到E世界：

// 一个N世界的方法
let add1 x == x + 1

// 一个被lift到E(Option)世界的方法
let add1IfPresent = Option.map add1

// 一个被lift到E(List)世界的方法
let add1ToEachElement = List.map add1

并在E世界使用了：

Some 2 |> add1IfPresent        // => Some 3
[1;2;3] |> add1ToEachElement   // => [2; 3; 4]

// 当然中间的变量大多数情况下都可以省了
Some 2 |> Option.map add1      // => Some 3
[1;2;3] |> List.map add1       // => [2; 3; 4]

|>类似Linux的Pipe（看日志不经常cat crm.log | grep 'xxx'嘛，就类似那个|）

我们怎么才能知道map实现是对的呢？什么才能称之为“对”的实现呢？，比如map加法的时候，肯定不能返回E世界的乘法，map变小写的肯定不能返回E世界变大写的函数。事实上，一个map要是对的，他必须满足一些规则（law）：

• map id 和 id 应该是一样的 （id 就是 identity方法，原样返回参数）
  
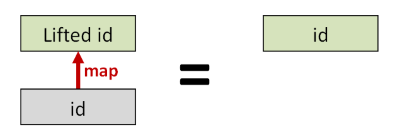
• map (f . g) 和 (map f) . (map g) 应该是一样的
  

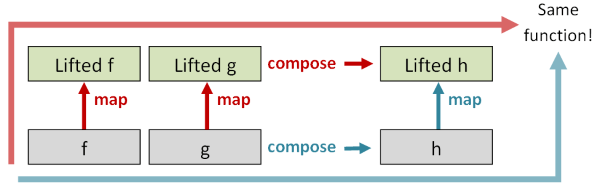
(f . g) x 相当于 f(g(x))，这个.就是compose

这俩规则就是Functor Laws，而所谓的Functor就是一个带map方法的type，比如E<T>。

诸如a->b的方法只在N世界存在，但很多时候我们需要的是跨世界的方法，比如拿一个id去查数据库，有可能查到也可能查不到：String -> Optional<User>，这种方法咋map呢，别急，再后面的文章就会讲这个东西。

return

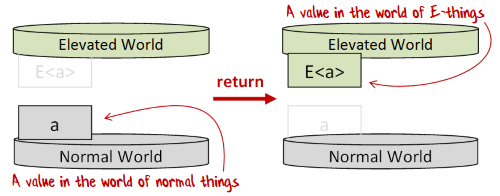
• 常见方法名： return, pure, unit, yield, point
• 作用：lift一个值到E世界
• Signature：a -> E<a>

这个就比较简单了，直接拿N世界的一个值创建一个E世界的值，举两例子：

// 一个被lift到E(Option)世界的值
// 'a -> 'a option
// 类似Java里的Optional.of()，Optional.empty()
let returnOption x = Some x

// 一个被lift到E(List)世界的值
// 'a -> 'a list
let returnList x  = [x]

apply

• 常见方法名： apply, ap, <*>
• 作用：把包在E<(a->b)>的值抽出来变成E世界方法E<a> -> E<b>
• Signature：E<(a->b)> -> E<a> -> E<b>

apply的另一种理解方式是一个两参函数，把a->b应用到E<a>内部并得到E<b>：

这个过程是可以无限套娃的，比如：

apply最大的作用是把N世界的多参函数变成E世界的多参函数

下面是分别Option和List的实现例子：

module Option =
    let apply fOpt xOpt =
        match fOpt,xOpt with
        | Some f, Some x -> Some (f x)
        | _ -> None

// [f;g] apply [x;y] => [f x; f y; g x; g y]
module List =
    let apply (fList: ('a->'b) list) (xList: 'a list)  =
        [ for f in fList do
          for x in xList do
              yield f x ]

通常都使用apply的中缀版，一般叫做<*>：

let resultOption =                 // => Some 5
    let (<*>) = Option.apply
    (Some add) <*> (Some 2) <*> (Some 3)
// resultOption =

let resultList =                   // => [11; 21; 12; 22]
    let (<*>) = List.apply
    [add] <*> [1;2] <*> [10;20]

有了apply和return，可以实现出map：

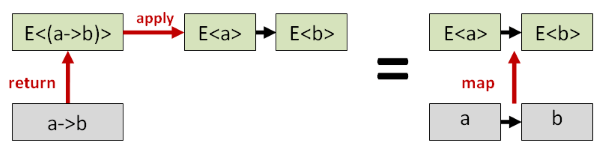
反之则不行，所以可以说apply和return的组合要比map更灵活。

因为map和apply . return是等同的，我们可以用map重写上面的例子：

let resultOption2 =                // => Some 5
    let (<!>) = Option.map         // 中缀版map
    let (<*>) = Option.apply

    add <!> (Some 2) <*> (Some 3)


let resultList2 =                  // => [11; 21; 12; 22]
    let (<!>) = List.map
    let (<*>) = List.apply

    add <!> [1;2] <*> [10;20]

这里的add <!> x <*> y和普通函数调用（add x y）长的很像了，唯一的区别在于这里的x和y是E世界的值。

和map一样，apply/return也要遵循一些规则，这些规则叫做Applicative Laws；有apply/return方法并满足这些规则的叫做Applicative Functor。

如下是其中的两个规则：

• apply . return . id 和 id 应该是一样的：
  
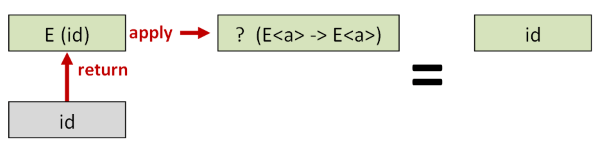
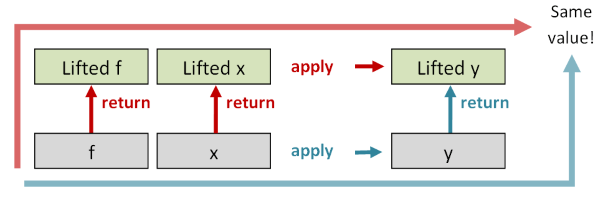
• return (apply f x) 和 apply (return f) (return x) 应该是一样的：
  

liftN

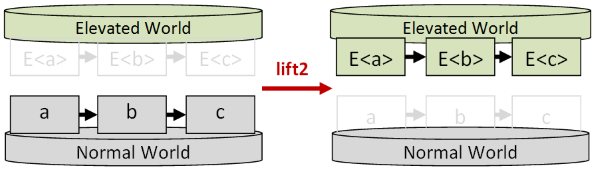
• 常见方法名： lift2, lift3, lift4 …
• 作用：map的多参数版本，用N世界函数组合多个E值
• Signature：lift2: (a->b->c) -> E<a> -> E<b> -> E<c>, lift3: (a->b->c->d) -> E<a> -> E<b> -> E<c> -> E<d>（lift1就是map）

liftN可以用map和apply轻松的定义出来：

module Option =
    let (<*>) = apply
    let (<!>) = Option.map

    let lift2 f x y =
        f <!> x <*> y

    let lift3 f x y z =
        f <!> x <*> y <*> z

    let lift4 f x y z w =
        f <!> x <*> y <*> z <*> w

// 两参函数的例子
let addPair x y = x + y
let addPairOpt = Option.lift2 addPair

addPairOpt (Some 1) (Some 2)  // => Some 3

lift2的另一种理解方式是作为“组合器”，比如：

Option.lift2 (+) (Some 2) (Some 3)   // Some 5
Option.lift2 (*) (Some 2) (Some 3)   // Some 6

这两个都是把后两个参数组合起来然后用第一个参数来决定怎么处理组合后的值。一个是加法，一个是乘法。

再进一步抽象的话，我们可以把“怎么处理”这个逻辑抽象出来，最简单的组合方式就是先用Tuple（Pair）包起来，后面再决定怎么处理：

let tuple x y = x,y

let combineOpt x y = Option.lift2 tuple x y
let combineList x y = List.lift2 tuple x y

let optTuple = combineOpt (Some 1) (Some 2)   // => Some (1, 2)
let listTuple = combineList [1;2] [100;200]   // => [(1, 100); (1, 200); (2, 100); (2, 200)]

有了E世界的tuple，“后面再决定怎么处理”的逻辑直接用map就行了：

optTuple |> Option.map (fun (x,y) -> x + y)   // => Some 5
listTuple |> List.map (fun (x,y) -> x * y)    // => [100; 200; 100; 400]

一个有趣的组合器是函数应用本身，我们可以用lift2来定义apply，有时候实现lift2比直接实现apply简单，这个就很有用了：

let apply fOpt xOpt =
    lift2 (fun f x -> f x) fOpt xOpt

有时候组合x,y时你只需要x或者只需要y，也就是半边的组合器：

let ( <* ) x y =
    List.lift2 (fun left right -> left) x y

let ( *> ) x y =
    List.lift2 (fun left right -> right) x y

<*和*>在Parser中很常见，比如你要读一个字符串token，你只想要引号中间的字符串，引号本身就不需要：

let readQuotedString =
   readQuoteChar *> readNonQuoteChars <* readQuoteChar

zip

• 常见方法名：zip, zipWith, map2, <*>
• 作用：把两个List用特定函数组合起来
• Signature：E<(a->b->c)> -> E<a> -> E<b> -> E<c>

一些类型可以有多个正确的apply实现，比如上面的List的apply是笛卡尔积，另一种实现是平行处理，称作zip：[f;g] apply [x;y] 相当于 [f x; g y]

let add x y = x + y

let resultAdd =
    let (<*>) = zip
    [add;add] <*> [1;2] <*> [10;20] // => [11; 22] / [(add 1 10); (add 2 20)]

这个例子说明了E世界并不只是每个类（比如List/Async），而是类+其抽象实现；上面的List世界（笛卡尔积）和zip世界背后都是List类型，但却有不同的实现。

Part 1 Summary

这一章主要讲了三个核心方法：map, return和apply；他们主要功能就是把N世界的东西lift到E世界里。

你可能觉得能实现这些方法的类不多，但其实不然，几乎所以的类都能实现这三个方法，比如你熟悉的Stream, List, Optional, Future等等。

在日常开发中我们写的很多方法都是跨世界方法（诸如a -> E<b>），下一章就要讲如何把跨世界的方法也lift到E世界了。