Last time we solved some graph problems using Union-Find, I mentioned that it can also be solved using graph traversal algorithms like DFS. In this series of article we’ll explore the idea of simple graph traversal algorithms like DFS and BFS, and try to solve more interesting problems. In case you didn’t know the basics of DFS go watch this.
Let’s first look at DFS. The idea behind it is simple: go down a path as deep as possible then backtrack as necessery and explore the rest of the branches. The algorithm itself is very clear and simple, the difficult part is:
- Identify the graph. Sometimes finding the graph itself IS the problem.
- Knowing when and how to mark the node as already been explored.
- Knowing when to backtrack. Sometimes we “don’t need” backtracking at all.
- Knowing when to stop and what to do when it happens.
- Knowing what to return and how to return it.
Let’s start with an easy problem: Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent using the mapping of a phone keyboard. E.g. “23” => [“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”]. At first glance their is no clear graph here, that’s because the graph is the answer. The letters are nodes and the answer is just all the paths in it:
def solve(digits)
mapping = { "2" => ["a", "b", "c"],
"3" => ["d", "e", "f"],
"4" => ["g", "h", "i"],
"5" => ["j", "k", "l"],
"6" => ["m", "n", "o"],
"7" => ["p", "q", "r", "s"],
"8" => ["t", "u", "v"],
"9" => ["w", "x", "y", "z"] }
dfs(digits, mapping)
end
def dfs(digits, m, k=0, path="", paths=[])
if k == digits.size
paths << path.dup
else
m[digits[k]].each do |c|
dfs(digits, m, k+1, path+c, paths)
end
end
paths
end
- When you see
m[digits[k]].eachit sure looks like BFS, but the recursion took care of it for us. In short, thinking in BFS. - We use
k+1as a way of marking nodes as already been explored. - We use
path+candpath.dupso that we don’t have to explicitly backtrack: every time we call dfs it creates a new string. You’ll see what I mean later. - We stop when we’ve processed all digits:
k == digits.size. And store current path in the result --paths. - In the end
pathswill contain all the paths and we simply return it.
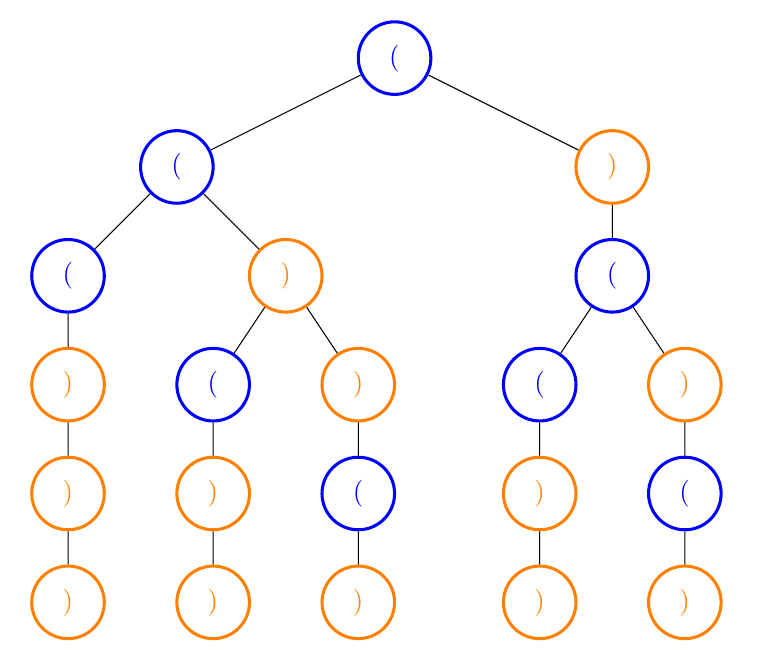
Let’s see another easy problem: given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses. E.g. n = 3 => [”((()))”, “(()())”, “(())()”, “()(())”, “()()()”].
def solve(n)
dfs(n, n)
end
def dfs(o, c, s="", paths=[])
return if o > c || c < 0 || o < 0
if o == 0
paths << "#{s}#{')'*c}"
else
dfs(o-1, c, s+"(", paths)
dfs(o, c-1, s+")", paths)
end
paths
end
The graph for n = 3 would look like this:
Now let’s look at a problem with explicit backtracking: Given a set of candidate numbers (candidates) (without duplicates) and a target number (target), find all unique combinations in candidates where the candidate numbers sums to target, e.g. given [2,3,5] and target 8, the result is [[2,2,2,2], [2,3,3], [3,5]]. Here is the code:
def solve(candidates, target)
return [] if candidates.empty?
dfs(candidates, target)
end
def dfs(c, t, k=0, sum=0, path=[], paths=[])
return if sum > t
if sum == t
paths << path.dup
else
(k..(c.size-1)).each do |i|
path << c[i]
dfs(c, t, i, sum+c[i], path, paths)
path.pop
end
end
paths
end
- We use
k..(c.size-1)because we don’t want to reuse the same sequence: given [2,3,5] and target 8, if we’ve already found 3+5, we don’t want to reconsider 5+3. - Recurring on
iso that we can reuse current number.
There is a variation of this problem in which case each number in candidates may only be used once in the combination. I’ll leave it to you.
Now back to the problem we saw last time in Union-Find:
- Search through all ‘O’s on border and mark them as ‘*’ (sinking the island).
- Flip all ‘O’s since it’s not connected to border.
- Flip all ‘*’s back to ‘O’.
def solve(board)
return if board.empty?
w, h = board[0].length, board.length
# step 1
(0...w).each do |j|
search(board, 0, j)
search(board, h-1, j)
end
(0...h).each do |i|
search(board, i, 0)
search(board, i, w-1)
end
# step 2 and 3
(0...h).each do |i|
(0...w).each do |j|
board[i][j] = 'X' if board[i][j] == 'O'
board[i][j] = 'O' if board[i][j] == '*'
end
end
end
# DFS
def search(board, i, j)
return if i < 0 || i > board.length-1 ||
j < 0 || j > board[0].length-1 ||
board[i][j] == 'X' || board[i][j] == '*'
board[i][j] = '*' # mark as visited
search(board, i-1, j) # up
search(board, i+1, j) # down
search(board, i, j-1) # left
search(board, i, j+1) # right
end
BFS and DFS each have their niche. DFS is good for cycle detection and can be used to implement an algorithm called topological sort, we’ll explore these ideas in part 2.